Eclipse FAQ

Some suggested questions and answers

What is a solar eclipse?

A solar eclipse occurs when the Moon's shadow falls on the Earth. The Moon is always casting a shadow, but it only hits the Earth when the Moon passes through the imaginary line between the Earth and the Sun, which can only happen at New Moon. [SVS 4390]

Why doesn't a solar eclipse happen at every New Moon?

Because the orbit of the Moon is tilted about 5 degrees. At most New Moons, the Moon is either above or below the Sun. Twice a year, the tilt is perpendicular to the Sun, making an eclipse possible. [SVS 4324]

Are solar eclipses dangerous?

No, not especially. It's always dangerous to stare at the Sun. It's just more likely that people will do this dangerous thing during an eclipse, since otherwise we don't have much reason to stare at the Sun. The danger is that the lens of the eye can focus intense sunlight onto a single point on the retina, causing permanent damage, and unfortunately, this process is mostly painless — you won't feel it happening.

Solar eclipse glasses with filters specifically designed for solar viewing will reduce the amount of light hitting your eye by a factor of 100,000 or more. The filters appear completely opaque when you're looking at anything other than the Sun. Wear the glasses during the partial phases of the eclipse. You need to take them off during totality, when the Sun is completely blocked by the Moon; otherwise, you won't see anything. See the Safety page elsewhere on this site.

What's the difference between the umbra and the penumbra?

The umbra and penumbra are different parts of the eclipse shadow. The penumbra is the partial shadow. It falls on places where the Sun is only partially covered by the Moon. The umbra is the full shadow, where the Moon has completely covered the Sun. The umbra is small and covers any given point on the Earth for only a few minutes before moving on. The penumbra is huge, usually covering a large fraction of the entire Earth. [SVS 4321]

What is totality?

Totality is the brief period of time during which the Moon completely or totally covers the Sun. During totality, you're standing inside the umbra and seeing the darkened sky, the solar corona, and even some stars. Totality lasts only a few minutes.

The path of totality is the path taken by the umbral shadow, the ground track of the total eclipse. If you're inside this path, the umbra will eventually pass over you, and you'll experience totality.

What are the different kinds of eclipses?

How often do eclipses occur?

Every year, there are at least two solar and two lunar eclipses. Some years, there can be up to five solar or five lunar eclipses, or a combined total of up to seven (five of one, two of the other, or four of one, three of the other).

But not all eclipses are equally interesting. Total eclipses happen somewhat less than once a year on average.

Is there a list or a catalog of eclipses?

There are several. Probably the most accessible is the Five Millennium Canon of Solar Eclipses by Fred Espenak and Jean Meeus. This work has charts and maps for every one of the 11,898 solar eclipses between 2000 BCE and 3000 CE. You can download it as a set of PDFs or browse the catalog online.

How accurate are eclipse predictions?

They're quite good, especially as we get closer to the event.

Lots of things can affect the accuracy of a complicated calculation, but eclipse predictions are generally accurate to within a city block or two and within about a second in both time and duration. The most detailed calculations can do even better — roughly 10 meters and a tenth of a second.

How fast does the Moon's shadow move?

The exact answer depends on the geometry of the eclipse. For the August, 2017 eclipse, the shadow moves from Oregon to South Carolina, a distance of almost 4000 kilometers (2500 miles), in about 90 minutes, an average speed of 2600 kph (1600 mph). That's about Mach 2.1 at airplane altitude! But that's an average. It moves a good deal faster at the beginning than it does later on, because the shadow is hitting the Earth at a more glancing angle.

Has the Moon's shadow ever been chased by a jet?

Yes, it has! During the June 30, 1973 eclipse, a French Concorde SST, the fastest commercial airliner ever flown, chased the shadow for 74 minutes at roughly Mach 2 while scientists on board conducted a variety of experiments. Several previous flights by scientists from the Los Alamos National Laboratory aboard a subsonic cargo jet were able to extend totality by just a few minutes.

Regular passenger flights have also intercepted the shadow path. Most recently, Alaska Airlines flight 870 flew through the shadow of the March, 2016 eclipse on its way from Anchorage to Honolulu. The flight plan was altered months in advance to give passengers a view of the eclipse from high above the clouds.

Does the Earth's rotation speed up the shadow or slow it down?

The rotation of the Earth slows the shadow down. The Earth spins in the same direction as the Moon orbits, so during an eclipse, it's as if the Earth is trying to keep facing the Moon, although it isn't fast enough. A point on the Earth's equator turns at about 1670 kph (1040 mph), but the Moon is moving at about 3600 kph (2200 mph) in its orbit.

The Earth and Moon are traveling at roughly 107,000 kph (67,000 mph) as they fly together around the Sun.

How are computers used to predict eclipses?

An ephemeris — a table of the positions of objects in the solar system over time — is used to search for the times when an eclipse is most likely to occur. For each of those times, a method invented by Friedrich Wilhelm Bessel in the 1820s is applied to the geometry of the Earth-Moon-Sun system to find the exact times and places where the Moon's shadow intersects the Earth's surface.

How is a solar system ephemeris calculated?

A simple ephemeris can be calculated by applying the principles of planetary motion discovered by Johannes Kepler in the early 1600s. Kepler found that every object in the solar system moves in an ellipse, and if you know the size, shape, and orientation of the ellipse, along with the position of the orbiting body at a single point in time, you can predict where that body will be at any other time.

But an orbit is only precisely elliptical if it's the only one in the solar system, and the solar system isn't that simple. To achieve the high accuracy required for precise eclipse prediction, we need to calculate the influence of gravity from each object on every other object.

Isaac Newton's gravity equation can only be solved for two bodies at a time, so the computer solves this equation for every possible pair of solar system objects and then sums the results. The speed and direction of each object is altered by the combined gravity of all of the others. The simulated solar system is allowed to move forward in time by a small time step, then the process is repeated.

After thousands, or even millions, of small time steps, you end up with a table of positions — an ephemeris — covering a long span of time. The Navigation and Ancillary Information Facility (NAIF) at NASA's Jet Propulsion Laboratory (JPL) publishes its Developmental Ephemeris (DE) series specifically for NASA mission planning, but the DE data is also used for everything from desktop planetarium programs to eclipse prediction.

What did Bessel contribute to eclipse prediction?

The math used to predict and map eclipses was first described by Friedrich Wilhelm Bessel in 1829 and was expressed in its modern form by William Chauvenet in 1863. Bessel's method uses a coordinate system based on a plane passing through the center of the Earth and perpendicular to the Sun-Moon line. This greatly simplifies the calculations. The intersection of the Moon's shadow with the plane is always a circle, for example, and its size depends only on the Moon's z-coordinate.

Using this coordinate system, it's possible to calculate just a handful of numbers, called Besselian elements, that can be plugged into various equations to predict almost anything you'd want to know about an eclipse. This was especially important in the 19th and early 20th centuries, when the math had to be done by hand. Even now, the simplicity of this approach allows us to compare hundreds or even thousands of eclipses far into the past and the future, using a reasonable amount of computer time.

Bessel's original papers (in German) are in Beiträge zur Theorie der Finsternisse und den Berechnungs-Methoden derselben, Astronomische Nachrichten No. 151 (7 Jan 1829) and No. 152 (7 Feb 1829). Chauvenet's contribution is in his Manual of Spherical and Practical Astronomy, vol. 1, beginning on page 439.

Has eclipse prediction improved since the days of Bessel and Chauvenet?

Absolutely. Our ability to predict the motions of solar system objects has improved dramatically during the Space Age. Better measurements, faster computers, and more sophisticated software that fully accounts for Albert Einstein's corrections to Newton all contribute to that improvement. Atomic clocks and radio astronomy allow us to measure the Earth's rotation with extreme precision. And global elevation maps of both the Earth and the Moon — maps derived from space-based sensors — are used to refine the timing of eclipse events.

How accurate is a modern solar system ephemeris?

It can be extremely accurate. By bouncing lasers off mirrors left on the Moon by Apollo astronauts (Apollo 11, 14 and 15) and Soviet rovers (Lunokhod 1 and 2), we can measure the Moon's distance to within a centimeter or less. When combined with Einstein's theory of gravity, this measurement provides a precise yardstick for the scale and mass of the entire solar system — we can both predict and actually see the periodic influence of Jupiter on the Earth-Moon system in the lunar laser ranging data!

What is a lunar limb profile and how is it used?

Bessel's method for predicting eclipses pretends that the Moon is a smooth sphere, when in fact its terrain is more rugged and extreme than the Earth's. The valleys along the silhouette edge, or limb, of the Moon affect the timing and duration of an eclipse by allowing sunlight to sneak through in places where a smooth Moon would block it. Eclipse calculations correct for this by using a limb profile, a description of the surface elevations around the disk of the Moon.

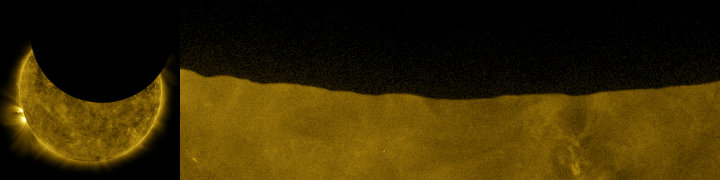Mountains and valleys near the south pole of the Moon are visible in this image of a partial solar eclipse taken from space by the Solar Dynamics Observatory spacecraft on October 7, 2010.

Until quite recently, everyone used the limb profiles published in 1963 by Chester Burleigh Watts. To produce his profiles, Watts designed a machine that traced some 700 photographs of the Moon covering the full range of angles, or librations, visible from Earth, an effort that spanned 17 years. Eclipse calculations are now moving to much more accurate limb profiles based on data from NASA's Lunar Reconnaissance Orbiter (LRO) and the Japan Space Agency's Kaguya spacecraft.

C.B. Watts's work on lunar limb profiles is described in Steven J. Dick's history of the U.S. Naval Observatory, Sky and Ocean Joined. The digitized Watts data is here.

How does the observer's height above sea level affect eclipse predictions?

During the 2017 eclipse, the high elevations of the Cascades and the Rockies shift the Moon's shadow to the southeast by more than a kilometer in some places, so for high accuracy, it's important to account for this. Some eclipse maps are accompanied by a table with correction factors for specific locations. Eclipse prediction programs that build in the elevation correction rely on digital elevation maps of the Earth such as SRTM, which was created from radar data collected during the February, 2000 flight of the Space Shuttle Endeavor.

Is the Earth's rotation really slowing down?

Yes. The rate at which it's slowing down is very small, but it adds up over time, enough that it affects eclipse predictions. In fact, the main source of uncertainty in the position of an eclipse is the very slightly irregular rotation of the Earth, something long suspected but not confirmed until 1939, by Harold Spencer Jones. Over the long term, the Moon, and to a lesser extent the Sun, are very slowly siphoning off the Earth's angular momentum through tidal friction. There are also shorter-term variations caused by things like glacial melt and motions in the interior of the Earth. Even major earthquakes can have a tiny effect.

The difference between a perfect clockwork Earth and the real one we live on is captured in a quantity called ΔT (delta tee). We can estimate ΔT for times in the distant past using ancient reports of eclipses. Our estimates improve dramatically for the four hundred years since the invention of the telescope. And an international team of scientists currently keeps track of the Earth's orientation on a daily basis — they're the folks responsible for deciding whether our clocks have gotten far enough out of sync with the Earth to require a leap second, something that's happened 27 times since 1972.

But we have no satisfactory theory for precisely predicting future values of ΔT. Each second of ΔT corresponds to 15 arcseconds of Earth rotation, or about 350 meters in east-west position at the mid-northern latitudes of the 2017 eclipse. Estimates should get us within a fraction of a second of the true value, but we won't know for sure until after the event. The farther we look into the future, or for that matter the past, the more uncertain we are about ΔT.

Another source of uncertainty may surprise you: the radius of the Sun. The standard value of the Sun's radius is 696,000 kilometers, and this is the value most often used in eclipse calculations. The calculation of eclipse durations is quite sensitive to small errors in this value. Near the point of greatest eclipse in 2017, for example, each second of duration corresponds to only 125 km of solar radius. So comparison of predictions to measurements of eclipse duration is a sensitive test of this value, and comparisons for recent eclipses suggest that the standard solar radius value may be too small by hundreds of kilometers.

Valid HTML 4.01 Strict Valid CSS 2.1